Home 프로그래머스 인공지능 데브코스 6주차 정리 및 후기
Post
Cancel

프로그래머스 인공지능 데브코스 6주차 정리 및 후기

Posted Oct 24, 2022 Updated Feb 18, 2023
By Seongchan Park
27 min read

이번 글에서는 프로그래머스 인공지능 데브코스의 6주차 강의에 대한 정리입니다.

1. 인공지능과 기계학습 소개

  • 일상 속 인공지능
    • 음성인식 (Siri), 추천 시스템 (Netfilx), 자율주행
    • 실시간 객체 인식 (Face ID), 로봇, 번역 (papago)
  • 데이터 기반의 접근
  • 기술에 집중하기 보다는, 인간 중심의 소통이 중요
  • 인공지능 == 도구
    • 도구를 만드는 방법을 배우는 것도 중요하지만, 도구를 사용하는 방법도 배워야 함


출처: https://itwiki.kr/w/%EC%9D%B8%EA%B3%B5%EC%A7%80%EB%8A%A5


  • 기계도 학습이 가능한가? 경험을 통해 점진적으로 성능이 향상되는 기계를 만들 수 있다!
  • 인공지능: 인간의 학습, 추론, 지각, 자연언어 이해 등의 지능적 능력을 기기로 실현한 기술
  • 학습: 경험의 결과로 나타나는, 비교적 지속적인 행동의 변화나 그 잠재력의 변화 또는 지식을 습득하는 과정
  • 경험 E를 통해, 주어진 작업 T에 대한, 성능 P의 향상 (E * T = P)
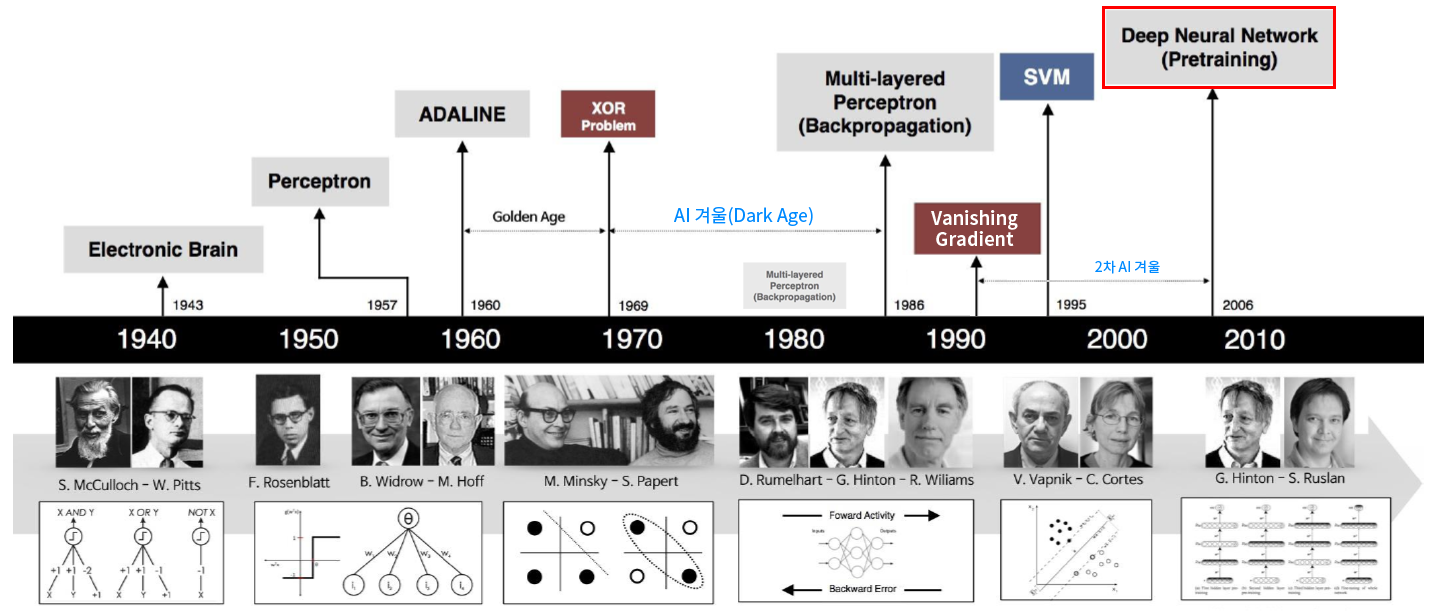
  • 인공지능의 주도권 전환
    • 지식 기반 -> 기계 학습 -> 심층 학습 (표현 학습, Deep learning, Representation learning)
    • 데이터 중심 접근 방식으로 전환
  • 예측은 회귀 (Regression) 문제와 분류 (Classification) 문제로 나뉨
    • 회귀는 목표치가 실수, 분류는 종류의 값

기계 학습 개념

  • 훈련집합 (Training set)
  • 가설: 눈대중으로 데이터 양상이 직선 형태를 보임 -> 모델을 직선으로 선택 가정
  • 기계 학습의 훈련 (Train)
    • 주어진 문제인 예측을 정확하게 할 수 있는 최적의 매개변수를 찾는 과정
    • 처음에는 임의의 매개변수로 시작하지만, 개선하여 정량적인 최적 성능 (Performance)에 도달
  • 훈련을 마치면, 추론 (Inference)을 수행
    • 새로운 특징에 대응되는 목표치의 예측에 사용
  • 기계 학습의 궁극적인 목표
    • 훈련집합에 없는 새로운 데이터에 대한 오류를 최소화 (새로운 데이터 = 테스트 집합)
    • 테스트 집합에 대한 높은 성능을 일반화 (Generalization) 능력이라 부름
  • 기계 학습의 필수 요소
    • 학습할 수 있는 데이터가 있어야 함
    • 데이터 규칙이 존재해야 함
    • 수학적으로 설명이 불가능
  • 차원의 저주 (Curse of Dimensionality): 차원이 높아짐에 따라 발생하는 현실적인 문제들
  • 기술 추세
    • 기계 학습 알고리즘과 응용의 다양화
    • 표현 학습이 중요해짐
    • 심층 학습이 기계 학습의 주류
    • 심층 학습은 현대 인공지능 실현에 핵심 기술
  • 인공지능의 단계: 초인공지능, 강인공지능, 약인공지능

데이터에 대한 이해

  • 데이터 수집 -> 모델 정립 (가설) -> 예측
  • 기계 학습: 데이터를 설명할 수 있는 학습 모델을 찾아내는 과정
  • 주어진 과업에 적합한 다양한 데이터를 충분한 양만큼 수집 => 과업 성능 향상

간단한 기계 학습의 예

  • 목적 함수 (비용 함수, Objective function, Cost function)
  • 과업을 달성하기 위해 모델의 성능이 개선되는지 객관적으로 확인할 수 있는 지표
  • 비용 함수의 예 중 하나는 평균제곱오차 (Mean Squared Error, MSE)
  • 비용 함수를 최소화 시킬 수 있는 파라미터를 찾는 것이 목표
  • 조금 더 현실적인 상황: 실제 세계는 선형 데이터가 아니고 잡음이 섞임 (비선형 모델이 필요)

모델 선택

  • 과소적합 (Underfitting): 모델의 용량 (자유도)이 작아서 오차가 클 수 밖에 없는 현상
    • 과소적합을 극복하기 위해서는 더 많은 데이터를 사용하거나, 비선형 모델을 사용하라
  • 과잉적합 (Overfitting): 고차원으로 근사한다면, 훈련 집합에 대해 거의 완벽하게 추정 가능
    • 하지만 새로운 데이터를 예측하는 경우에는 문제가 발생할 수 있음
    • 모델의 용량이 크기 때문에 학습 과정에서 잡음까지도 학습해버림

  • 따라서 적절한 용량의 모델을 선택하는 모델 선택 작업이 필요함

  • 편향 (Bias)과 분산 (변동, Variance) => trade-off 관계
    • 훈련집합을 여러 번 수집하여 1~12차에 반복해서 적용하는 실험
    • 저차원에서는 오차가 크고, 편향도 큼. 하지만 비슷한 모델을 얻음 (낮은 변동)
    • 고차원에서는 오차가 작고, 편향도 작음. 하지만 크게 다른 모델을 얻음 (높은 변동)
    • 용량이 작은 모델 (과소적합)은 편향이 크고, 분산이 작음
    • 용량이 복잡한 모델 (과대적합)은 편향이 작고, 분산이 큼
  • 기계 학습의 궁극적인 목표
    • 낮은 편향과 낮은 분산을 가진 예측 모델을 만드는 것이 목표
    • 하지만 모델의 편향과 분산은 상충 관계
    • 따라서 편향을 최소로 유지하며, 분산도를 최대로 낮추는 전략이 필요함
    • 모델의 용량이 증가한다는 것은 편향이 감소하고, 분산이 증가하는 경향이 있음
  • 검증집합을 이용한 모델 선택
    • 훈련집합과 테스트집합과 다른 별도의 검증집합 (Validation set)을 가진 상황
  • 부트스트랩 (Bootstrap)
    • 임의의 복원 추출 샘플링 (Sampling with replacement) 반복
    • 데이터 분포가 불균형 일 때 사용
  • 현대 기계 학습의 전략
    • 용량이 충분히 큰 모델을 선택한 후에,
    • 선택한 모델이 정상을 벗어나지 않도록 여러 규제 (Regularization) 기법을 적용
      • 데이터 확대: 데이터를 많이 수집할수록 일반화 능력이 향상됨
      • 가중치 감쇠: 개선된 목적함수를 이용하여 가중치를 작게 조절하는 규제 기법

지도 방식에 따른 유형

  • 지도 학습 (Supervised Learning)
    • 특징 벡터와 목표치 (정답)가 모두 주어진 상황
    • 회귀와 분류 문제로 구분
  • 비지도 학습 (Unsupervised Learning)
    • 특징 벡터는 주어지는데, 목표치가 주어지지 않는 상황 (정답이 없음)
    • 군집화 (Clustering), 밀도 추정 (Density estimation), 특징 공간 변환 (PCA) 과업
  • 강화 학습 (Reinforcement Learning)
    • 상대적인 목표치가 주어지는데, 지도 학습과 다른 형태 (보상)
  • 준지도 학습 (Semi-supervised Learning)
    • 일부는 특징 벡터와 목표치를 모두 가지지만, 나머지는 특징 벡터만 가지는 상황
    • 최근, 대부분의 데이터가 특징 벡터 수집은 쉽지만, 목표치는 수작업이 필요하여 최근 중요성 부각

다양한 기준에 따른 유형

  • 오프라인 학습과 온라인 학습 (Offline, Online Learning)
    • 보통은 오프라인 학습을 다룸
    • 온라인 학습은 IoT 등에서 추가로 발생하는 데이터 샘플을 가지고 점증적 학습 수행
  • 결정론적 학습과 확률적 학습 (Deterministic, Stochastic Learning)
    • 결정론적에서는 같은 데이터를 가지고 다시 학습하면 같은 예측 모델이 만들어짐
    • 확률적 학습은 학습 과정에서 확률 분포를 사용하므로, 같은 데이터로 학습하면 다른 예측 모델이 나옴
  • 분별 모델과 생성 모델 (Discriminative, Generative Models)
    • 분별 모델은 부류 예측에만 관심. 즉, P(y|x)의 추정에 관심
    • 생성 모델은 P(x) 또는 P(x|y)를 추정하여 새로운 샘플을 생성하여 사용할 수 있음

2. 기계학습과 수학 리뷰

기계학습에서 수학의 역할

  • 수학은 목적함수를 정의하고, 목적함수의 최저점을 찾아주는 최적화 이론 제공
  • 최적화 이론에 학습률, 멈춤 조건과 같은 제어를 추가하여 알고리즘 구축

벡터와 행렬

  • 백터 (Vector): 샘플을 특징 벡터 (Feature vector)로 표현
  • 행렬 (Matrix): 여러 개의 벡터를 담음, 훈련 집합을 담은 행렬을 설계 행렬 (Design matrix)이라고 부름
    • 전치 행렬 (Transpose matrix): 행 요소와 열 요소를 뒤바꾼 것
  • 행렬을 이용하면, 방정식을 간결하게 표현 가능
  • 특수 행렬들
    • 정사각행렬 (정방행렬, Square matrix)
    • 대각행렬 (Diagonal matrix)
    • 단위행렬 (Identity matrix)
    • 대칭행렬 (Symmetrix matrix)
  • 행렬 연산: 행렬 곱셈, 벡터의 내적 (Inner product)
  • 텐서 (Tensor): 3차원 이상의 구조를 가진 숫자 배열 (array)
    • 0차: 수 (Scalar), 1차: 벡터 (Vector), 2차: 행렬 (Matrix)
  • 유사도 (Similarity)와 거리 (Distance): 벡터를 기하학적으로 해석 (코사인 유사도)
  • 벡터와 행렬의 거리 (크기)를 놈 (Norm)으로 측정
    • 행렬의 프로베니우스 놈 (Frobenius norm)으로 행렬의 크기 측정 가능
    • 1차 놈 (Manhattan distance)
    • 2차 놈 (Euclidean distance)

퍼셉트론의 해석

  • 퍼셉트론 (Perceptron): 1958년에 고안한 분류기 (Classifier) 모델, 활성 함수는 계단 함수 사용
  • 다중 퍼셉트론 (Multi-layer perceptron)
  • 추론 (Inferring)은 학습을 마친 알고리즘을 현장의 새로운 데이터에 적용하는 작업
  • 훈련 (Training)은 훈련 집합의 샘플에 대하여 가장 잘 설명할 수 있는 가중치를 찾아내는 작업
    • 현대 기계학습에서 심층학습은 퍼셉트론을 여러 층으로 확장하여 만듦

선형결합과 벡터공간

  • 벡터: 공간 상의 한 점으로 화살표 끝이 벡터의 좌표에 해당
  • 선형결합이 만드는 벡터공간: 기저 벡터 a와 b의 선형 결합 (Linear combination)
  • 선형결합으로 만들어지는 공간을 벡터공간 (Vector space)이라고 부름

역행렬

  • 다음의 성질은 서로 필요충분조건
    • A는 역행렬을 갖음. 즉, 특이행렬이 아님
    • A는 최대계수를 갖음
    • A의 모든 행과 열이 선형독립임
    • A의 행렬식은 0이 아님
    • A의 고윳값은 모두 0이 아님

행렬 분해

  • 분해 (Decomposition): 정수 3717은 특성이 보이지 않지만, 3*3*7*59로 소인수 분해하면 특성이 보임
  • 고윳값 (Eigenvalue), 고유 벡터 (Eigenvector)
  • 고유 분해 (Eigen-decomposition)는 고윳값과 고유 벡터가 존재하는 정사각행렬에만 적용 가능
    • 하지만 기계학습에서는 정사각행렬이 아닌 경우의 분해도 필요하기 때문에 고유 분해는 한계가 있음
    • 특잇값 분해 (Singular Value Decomposition, SVD) 등장 - 정사각행렬이 아닌 행렬의 역행렬 계산에 사용

확률과 통계

  • 기계학습이 처리할 데이터는 불확실한 세상에서 발생하므로, 불확실성 (Uncertainty)을 다루는 확률 및 통계가 필수
  • 확률 변수 (Random variable)
  • 확률 분포 (Probability distribution): 확률질량함수 & 이산확률변수, 확률밀도함수 & 연속확률변수
  • 확률 벡터 (Random vector): 확률변수를 요소로 갖음
  • 확률 기초: 곱 규칙 (Product rule), 합 규칙 (Sum rule)
    • 조건부 확률, 연쇄법칙 (Chain rule), 독립 (Independence), 조건부 독립, 기댓값

베이즈 정리와 기계학습

  • 베이즈 정리 (Bayes’ rule)
  • 사후 (Posteriori) 확률 = 우도 (Likelihood) 확률 * 사전 (Prior) 확률
  • 사후 확률을 직접 추정하는 일은 아주 단순한 경우를 빼고 거의 불가능
  • 따라서 베이즈 정리를 이용하여 추정

최대 우도

  • 매개변수 (모수, Parameter)를 모르는 상황에서 매개변수를 추정하는 문제
  • 어떤 확률변수의 관찰된 값들을 토대로 그 확률변수의 매개변수를 구하는 방법 (최대 우도, Maximum Likelihood)

평균과 분산

  • 데이터의 요약 정보로서 평균 (Mean)과 분산 (Variance)
  • 평균 벡터 (치우침 정도)와 공분산 행렬 (Covariance matrix) - 확률변수의 상관정도

유용한 확률분포

  • 가우시안 분포 (Gaussian distribution): 평균과 분산으로 정의
    • 다차원 가우시안 분포: 평균 벡터와 공분산행렬로 정의
  • 베르누이 분포 (Bernoulli distribution): 성공 확률 p이고, 실패 확률이 1-p인 분포
  • 이항 분포 (Binomial distribution): 성공 확률이 p인 베르누이 실험을 m번 수행할 때, 성공할 횟수의 확률분포
  • 로지스틱 시그모이드 함수 (Logistic Sigmoid function): 일반적으로 베르누이 분포의 매개변수를 조정을 통해 얻음
  • 소프트플러스 함수 (Softplus function): 정규 분포의 매개변수의 조정을 통해 얻음
  • 지수 분포 (Exponential distribution)
  • 라플라스 분포 (Laplace distribution)
  • 디랙 분포 (Dirac distribution)
  • 혼합 분포들 (Mixture distribution): 3개의 요소를 가진 가우시안 혼합 분포
  • 변수 변환 (Change of variables): 기존 확률변수를 새로운 확률변수로 바꾸는 것

정보이론

  • 정보이론: 사건 (Event)이 지닌 정보를 정량화 할 수 있을까?
    • 정보이론의 기본 원리: 확률이 작을수록 많은 정보
    • 자주 발생하는 사건보다, 잘 일어나지 않는 사건 (Unlikely event)의 정보량 (Informative)이 많음
  • 정보이론과 확률통계는 많은 교차점을 가짐, 확률통계는 기계학습의 기초적인 근간 제공
  • 정보이론 관점에서도 기계학습을 접근 가능: 엔트로피, 교차 엔트로피, KL 발산, 상대 엔트로피
  • 자기 정보 (Self information): 사건 (메시지)의 정보량
  • 엔트로피 (Entropy): 확률변수 x의 불확실성을 나타내는 엔트로피, 모든 사건 정보량의 기댓값으로 표현
    • 모든 사건이 동일한 확률을 가지 때 즉, 불확실성이 가장 높은 경우에 엔트로피가 최고임
  • 교차 엔트로피 (Cross entropy): 두 확률분포 P와 Q 사이의 교차 엔트로피
    • 심층학습의 손실함수로 많이 사용
    • 교차 엔트로피를 손실함수로 사용하는 경우, KL 발산의 최소화 함과 동일
    • KL 다이버전스: 두 확률분포 사이의 거리를 계산할 때 주로 사용
    • 가지고 있는 데이터 분포 P(X)와 추정한 데이터 분포 Q(X) 간의 차이를 최소화하는데 교차 엔트로피 사용

최적화

  • 기계학습의 최적화는 단지 훈련집합이 주어지고,
  • 훈련집합에 따라 정해지는 목적함수의 최저점으로 만드는 모델의 매개변수를 찾아야 함
  • 주로 확률적 경사 하강법 (Stochastic gradient descent, SGD) 사용

매개변수 공간의 탐색

  • 특징 공간의 높은 차원에 비해 훈련 집합의 크기가 작아서 참인 확률분포를 구하는 일은 불가능
  • 따라서 기계학습은 적절한 모델 (가설)을 선택하고, 목적함수를 정의하여 모델의 매개변수 공간을 탐색
  • 그리고 목적함수가 최저가 되는 최적점을 찾는 전략 사용
  • 특징 공간에서 해야 하는 일을 모델의 매개변수 공간에서 하는 일로 대치
    • 최적화 문제 해결: 낱낱 탐색 (Exhaustive search) 알고리즘, 무작위 탐색 (Random search) 알고리즘
      • 경사 하강법 (미분 활용)

미분

  • 미분에 의한 최적화: 1차 도함수는 함수의 기울기 (경사), 즉 값이 커지는 방향을 지시
  • 편미분 (Partial derivative): 변수가 복수인 함수의 미분, 미분 값이 이루는 벡터를 경사도라고 부름
  • 기계학습에서 편미분: 매개변수 집합은 복수 매개변수이므로, 편미분을 사용
  • 최적화는 예측 단계가 아닌, 학습 단계에서 필요함

경사 하강 알고리즘

  • 경사 하강법 (Gradient descent)는 낮은 곳을 찾아가는 원리
    • 함수의 기울기 (경사)를 구하여 기울기가 낮은 쪽으로 반복적으로 이동하여 최솟값에 도달
  • 집단 (무리, Batch) 경사 하강 알고리즘
    • 샘플의 경사도를 구하고 평균한 후에 한꺼번에 갱신
    • 훈련 집합 전체를 다 봐야 갱신을 일어나기 때문에 학습 과정이 오래 걸린다는 단점 존재
    • 정확한 방향으로 수렴하긴 하지만, 속도가 느리다는 단점
  • 확률론적 경사 하강 (SGD, Stochastic Gradient Descent) 알고리즘
    • 한 샘플 혹은 작은 집단 (무리, Mini-batch)의 경사도를 계산한 후 즉시 갱신
    • 수렴이 다소 해맬 수도 있긴 하지만, 속도가 빠르다는 장점

3. ML Basics - E2E

End to End 머신러닝 프로젝트

  1. 큰 그림 보기
    • 문제 정의: 지도학습 & 비지도학습, 분류문제 & 회귀문제, 배치학습 & 온라인학습
    • 성능측정지표: RMSE 등
  2. 데이터를 구하기
    • 데이터 가져오기
    • 데이터 구조 훑어보기
    • train, test 데이터셋 나누기 (데이터 변경이 생겨도 일관성 있는 기준을 유지하도록 하라)
  3. 데이터로부터 통찰을 얻기 위해 탐색하고, 시각화 해보기
    • 상관관계 확인
  4. 머신러닝 알고리즘을 위해 데이터를 준비하기
    • 데이터 수동 변환 보다는, 함수를 만들어서 자동 변환하는 것이 더 좋음
    • 새로운 데이터에 대한 변환을 손쉽게 재생산 할 수 있음
    • 향후 재사용할 수 있는 라이브러리 구축 가능 - 데이터 정제 (Data Cleansing)
    • 누락된 특성 다루는 방법: 행 제거, 열 제거, 특정 값으로 채우기 (0, 평균, 중간값 등)
    • SimpleImputer 함수 활용하기
    • One hot 인코딩 (OrdinalEncoder, OneHotEncoder 함수 활용하기) - 특성 스케일링 (Feature Scaling): Min max scaling, Standardization - 변환 파이프라인 (Transformation Pipeline): 순차적 변환 시, 사용 (Pipeline class)
  5. 모델을 선택하고 훈련시키기
  6. 모델을 상세하게 조정하기
  7. 솔루션을 제시하기
  8. 시스템을 론칭하고, 모니터링 및 유지보수 하기

4. ML Basics - Linear Algebra

  • 행렬의 곱셈
  • 중요한 연산과 성질들 (정방행렬, 삼각행렬, 대각행렬, 단위행렬)
  • Norms
  • 선형독립과 Rank
  • 역행렬, 직교행렬
  • 행렬식
  • 이차형식
  • 고유값, 고유벡터
  • 행렬미분

5. 6주차 돌아보기

  • 기간: 2022. 10. 24 ~ 2022. 10. 29



출처: 프로그래머스 인공지능 데브코스 4기 6주차 강의 -> 강의 내용 정리 깃허브 링크

Education, 프로그래머스 인공지능 데브코스 4기
AI Deep learning Machine learning 프로그래머스 인공지능 데브코스 K-digital training
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

AI 학습용 데이터 라벨링 교육 - 데이터 기획 과정

프로그래머스 인공지능 데브코스 7주차 정리 및 후기