 |  |
간단한 책 소개
이 책은 머신러닝 분야 속에서 기초가 되는 기초 통계와 활용 기법을 소개하고 있습니다.
‘R’이라는 프로그래밍 언어를 활용하여 모델링과 예측 기법들을 Lab 문제로 확인해 볼 수 있는데,
이 블로그에서는R 언어 뿐 아니라, 같은 내용을 Python으로도 적용해보는 것을 목표로 기록해보려고 합니다.
인공지능 분야에서도 기초가 되는 머신러닝 내용들을 복습하며, 개념들을 다시 정리할 것입니다.
이 책을 정리한 후에는 머신러닝 및 딥러닝 분야에 대해서도 기록해볼 예정입니다.
| Chapter | Title | Main Topics |
|---|---|---|
| 1강 | 도입 (Introduction) | 통계학습 개요 및 역사, 표기법 설명 |
| 2강 | 통계학습 (Statistical Learning) | 통계학습 개념, 지도 및 비지도학습, 회귀 및 분류, 모델 평가 |
| 3강 | 선형회귀 (Linear Regression) | 단순선형회귀, 다중선형회귀, K-최근접이웃 |
| 4강 | 분류 (Classification) | 로지스틱회귀, 선형판별분석, LDA, QDA, KNN |
| 5강 | 재표본추출 방법 | 교차검증 (Cross-Validation), 붓스트랩, K-fold |
| 6강 | 선형모델 선택 및 정규화 | Lasso, 차원축소, 주성분회귀 |
| 7강 | 선형성을 넘어서 | 다항식회귀, 회귀 및 평활 스플라인, 일반화가법모델 |
| 8강 | 트리 기반의 방법 | 의사결정트리, 배깅, 랜덤포레스트, 부스팅 |
| 9강 | 서포트 벡터 머신 (SVM) | 최대 마진 분류기, 서포트 벡터 분류기, 로지스틱 회귀에 대한 상관관계 |
| 10강 | 비지도학습 | 주성분 분석, 클러스터링 (K-평균, 계층적) |
1.1 통계학습의 개요
통계학습 (Statistical Learning)은 데이터에 대한 이해를 위한 방대한 도구 집합을 뜻한다.
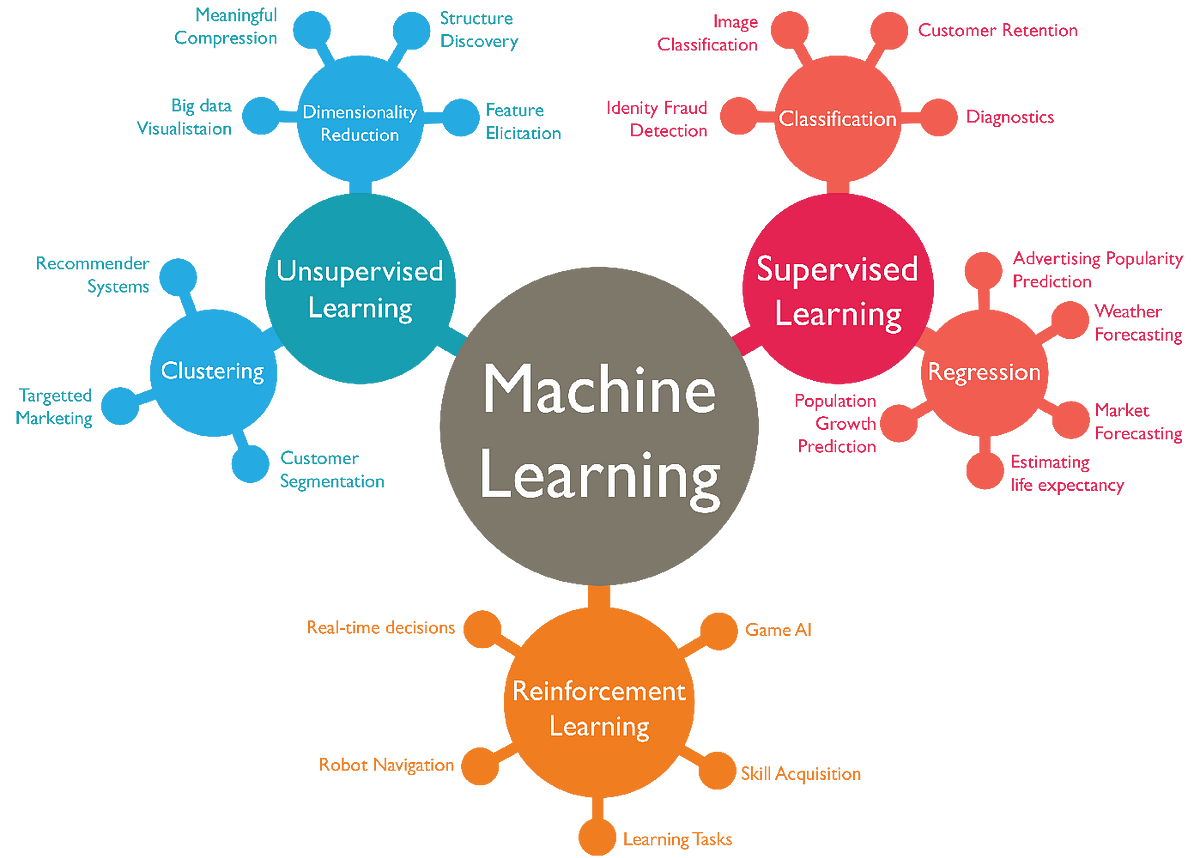
이러한 도구들은 지도 (Supervised) 학습과 비지도 (Unsupervised) 학습으로 분류될 수 있다.
- 지도 학습: 하나 이상의 입력 변수를 기반으로 출력 변수를 예측하거나 추정하는 통계적 모델을 만드는 것
- 비지도 학습: 출력 변수 없이 입력 변수만 있지만 자료의 상관관계와 구조를 파악할 수 있는 것
그렇다면,
통계학습 (Statistical Learning)과 기계학습 (Machine Learning)의 차이는 무엇일까요?
책에서도 경계를 명확히 나누지 않고, 두 분야 사이에 밀접한 연관성도 있지만 호기심을 가지고 조금 찾아 보았습니다.
일반적으로 두 학습 방식들 모두 데이터에 의존적이라는 공통점이 있을 것입니다.
하지만 통계학습은 변수 사이의 관계 등과 같이 rule-based approach 이라는 측면이 있다고 하면,
기계학습은 기계가 데이터를 통해 스스로 학습한다는 측면에서 명시적인 프로그래밍으로 접근하지는 않습니다.
또한 많은 양의 데이터를 통해 학습이 이뤄지는 기계학습은 지도 및 비지도 학습에 조금 더 포커스를 맞춘다고 하면,
비교적 적은 데이터를 다루는 통계학습은 표본이나 모집단, 가설 등과 같은 통계적 개념들로 접근한다고 할 수 있습니다.
결국, 통계학습은 통계학을 기반으로 하여 해석의 영역에 있어서 유의미하게 적용이 될 수 있을 것이고,
반대로 기계학습은 사람의 노력을 최소화 한 상태에서 숨겨진 패턴 등을 발견하는데 유용하게 사용될 수 있을 것입니다.
참고 - Machine Learning VS. Statistical Learning
1.2 통계학습의 간단한 역사
통계 및 기계학습이라는 용어는 어색할 수 있지만, 이 분야의 기초가 되는 개념들은 오래 전에 개발되었다.
19세기 초반 르장드르와 가우스는 최소제곱법에 대한 논문을 발표하면서, 지금은 선형회귀로 알려진 형태를 구현했다.
양적 데이터에 적용되는 선형회귀를 기반으로 질적 데이터에 적용할 수 있도록 피셔는 1936년 선형판별분석을 제안했다.
1940년대에는 대안적인 방법으로 로지스틱 회귀가 제안되었고, 1970년대 초에는 일반화된 선형모델들이 정의되었다.
1980년대 중반에는 브라이먼, 프리드먼, 올쉔, 스톤이 분류 및 회귀 나무를 도입했고,
해스티와 티브시라니는 1986년에 일반화된 선형모델의 비선형적 확장에 대해 일반화가법모델을 제안했다.
1.3 표기법과 간단한 행렬 대수
데이터 표본에서 데이터 포인트 수나 관측치 수는 n으로 사용하고, 예측하는데 사용하는 변수들의 수는 p로 사용한다.
일반적으로 i번째 관측치에 대한 j번째 변수의 값은 x_ij로 표현하며, X는 n * p 행렬을 나타낸다.
이를 바탕으로 기본적인 행렬 및 벡터에 대한 개념, 전치 (Transpose), 행렬 연산 등을 다루게 된다.
1.4 Lab과 연습문제에 사용된 자료
이 책에서는 통계학습 방법들을 마케팅, 금융, 생물학, 그리고 다른 분야에 적용하여 설명한다.
Lab과 연습문제에서 사용한 자료 리스트 및 추가적인 자료들은 ISLR 라이브러리에서 참고할 수 있다.
